HAPPY NEW YEAR!!!! Yeah I'm 12 days late but, eh, whatever. As the "New year new me" doctrine insinuates, a new year must call for new nerdy things to geek out about. First one of this year is... well, network theory, if you couldn't tell. Ok so technically I had already been geeking out about network theory before the new year but sshhhhhh.
Anywho, TRANSITION
Suppose you lived in a perfect world. In this world, each and every person has only 3 friends (and we'll ignore the possibility of friend circles). Suppose you were to count how many friends you have (which would be 3) and then count all of your friend's friends (9), and so on and so forth how ever many times you like. How many friends would there be in total? Well, let's dive right into it.
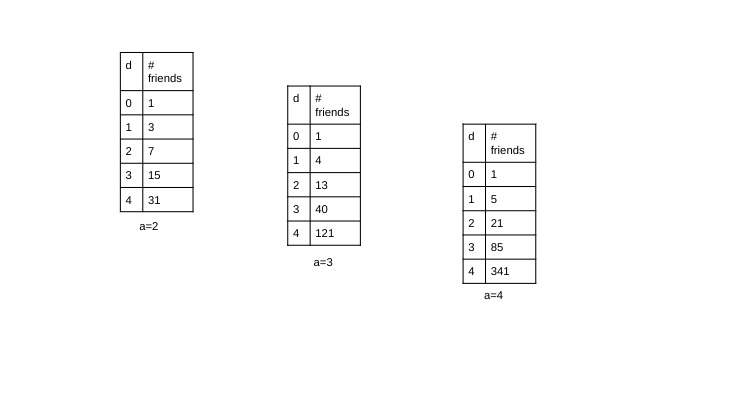
So, the distance one friend is from you will be considered the "degree" of the friendship, so your closest friends would be first degree friends, and their friends would be your second degree friends, and so on and so forth. And, just so the math will turn out nice, we will be counting yourself as your own 0th degree friend :). Ok, let's take this previous 3 friend example, and suppose we want to count the total number of friends up to the 3rd degree. So you have yourself, 1, then your 3 friends, and a group of 3 friends per each of your 3 first degree friends, so 9 second degree friends. And then, another group of 3 friends per 9 second degree friends, 27. Add all of these up and you get 40 friends! Wow! Do you notice a pattern with these values per degree? Yup, each were powers of 3, which is the number we chose to be # of friends per person. So we can rewrite the entirety of this scenario as 3^0 + 3^1 + 3^2 + 3^3 = 40. Ok, we now have a starting model for how we can treat this problem. It's the sum of all the powers of three up to the degree we choose to stop counting. From here on out we will label the number of friends per person as "a" (or the sensitivity), and the degree we choose to stop counting as "d" (or the degree limit). So far our problem can be written as the sum of the seires a^k as k increases incrementally by 1 to d. We can also write tables for some a value as we choose to increase d, we can list d on the x column and the total friends as y. Here are some example tabels for differeing a values:

Orci dapibus ultrices in iaculis nunc sed augue lacus. Viverra aliquet eget sit amet tellus. Et ligula ullamcorper malesuada proin libero. Lectus vestibulum mattis ullamcorper velit. Sapien pellentesque habitant morbi tristique. Vestibulum sed arcu non odio euismod. Nibh mauris cursus mattis molestie a iaculis at erat. Vitae tortor condimentum lacinia quis vel eros donec ac. In cursus turpis massa tincidunt dui ut ornare lectus sit. Sed vulputate odio ut enim blandit volutpat. Vitae congue eu consequat ac.
Iaculis nunc sed augue lacus viverra vitae congue. Viverra ipsum nunc aliquet bibendum enim facilisis gravida neque convallis. A diam sollicitudin tempor id eu nisl. Nunc sed blandit libero volutpat sed. Risus at ultrices mi tempus imperdiet nulla malesuada pellentesque elit. Justo laoreet sit amet cursus sit amet dictum. Adipiscing elit duis tristique sollicitudin nibh sit. Sed vulputate odio ut enim blandit volutpat. Neque gravida in fermentum et sollicitudin ac orci phasellus. Euismod quis viverra nibh cras pulvinar mattis nunc sed blandit.